פתרון חידות 22-29: לחץ/י כאן

פתרון חידות 15-21: לחץ/י כאן

פתרון חידות 9, 12-14 ורשימת הפותרים: לחץ/י כאן

פתרון חידות 5-7/2021 ורשימת הפותרים : לחץ/י כאן

פתרון חידות 3-4/2021: ורשימת הפותרים לחץ/י כאן

פתרון חידות 1-2/2021: ורשימת הפותרים לחץ/י כאן

*************************************************************

פתרון חידה 1/2020

אורך צלע המשולש מקיים  a

1 =a/√3+a(1+2+ 3)+ 3a/√3

ומכאן

a=1/(6+4/√3)=0.12

פתרון חידה 2/2020

מקבלים ממשפט פיתגורס משוואה ריבועית עבור הצלע המבןקשת של המשולש הקטן

q² +(✓3/2)rq-3r²/4 = 0,

ולכן

q =  r[-√3/2+✓(3/4+16/3)]=  √3(√5 -1)=0.5352

 

פתרון חידה 3/2020

אורך אלכסון הריבוע מקיים

2r✓2 + 3r + r✓2 = ✓2

לכן

r=(2-✓2)/3 = 0.195

פתרון חידה 4/2020

4a  מציינת את אורך צלע הריבוע.  היקף הריבוע-   –  a

– רדיוס המעגל  מקיים r

r = ( 5/8)a

היקף המעגל הוא לכן

( 5/8)a.2π =3.927a

לכן היקף הריבוע גדול מהיקף המעגל.

פתרון חידה 5/2020

מחישוב שטח המשולש יוצא

c  = ab/h

 a²b² ב  וחילוק  במשפט פיתגורס c ע"י הצבת מתקבלת התוצאה.

פתרון חידה 6/2020

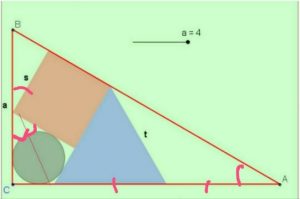
מניתוח הנתונים מקבלים שזוויות המשולש ABC הן 90⁰, 60⁰, 30⁰ בהתאמה  .

יוצא שהזוויות המסומנות בשירטוט הנילווה הן כולן בנות 30⁰.  לכן אורך היתר במשולש  הפנימי העליון הוא  2s/√3  .  מכאן מקבלים

a = s + 2s/✓3  ,   t =  s + s/√3

ובסה"כ :

s = a√3(2 – √3)=0.464a

t = a (√3 – 1)=0.732a

 

פתרון חידה 7/2020

 

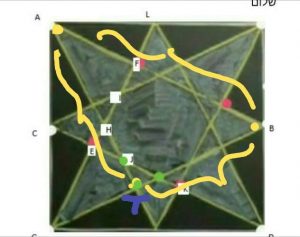
מהנתונים ומשפט פיתגורס יוצא שהאורך t של "אלכסון" ארוך כגון AB מקיים

t  = |AB|=(a√5)/2 …………………………………….  [I]

שוויון הזוויות הנוצרות בבנייה גורר דמיון של משולשים רלבנטיים ולכן  שמונה המשולשים ה"שחורים" , כגון AFL, הם ישרי זווית ודומים למשולש  הבסיסי  5√:2 :1, כשהיתר שלהם הוא a/2.

|FL|= a/(25√) =t/5 …………………………………….  [II]

|AF|= 2|FL| = a/5√ = (a√5)/ 5 =2t/5 …………………………………….  [III]

א. השטח s של משולש "שחור" הוא  S = |AF|.|FL|/2 = a²/20.

ע"י החסרת שטחי שמונת המשולשים השחורים משטח הריבוע מתקבל שטח המצולע הכוכבי

a²  –  8.a²/20 = 0.6a²

ב'.  לחישוב שטח הריבוע ה"וורוד" נשים לב לחלוקה ההדדית של האלכסונים הגדולים, דוגמת AB,  ראינו ב [I] שאורך AF מהווה שתי חמישיות מאורך האלכסון AB . ומצידו השני נגרעה מהאלכסון חמישית נוספת מאורכו. אורך צלע הריבוע הוא 2/5 מאורך האלכסון שכבר חושב לעיל ולכן השטח המבוקש הוא

(2t /5)²  = ( 2 a√5/(2.5))² =  a²/5

ג'.  נציג כאן את הדרך המשתמשת בדמיון משולשים. אפשר לפתור גם בעזרת חשבון זוויות וטריגונומטריה. המפתח נעוץ בהבנה שהמשולש ירוק הקודוקדים מהשאלה דומה למשולש המסומן בצהוב בשירטוט המצורף , כלומר למשולש ישר הזווית ABT . כשכזכור אורך היתר AB הוא  t.  ניווכח שקיבלנו משולש "פיתגוראי" עם יחסי צלעות 3:4:5,      BT|=(3/5)t|,   AT| =( 4/5)t|  ,  AB| = t = ( 5/5)t|  , ראו [I]  לעיל.

מכיוון שסכום אורכי שלוש הצלעות של המשולש המבוקש הוא בדיוק אורך צלע של הריבוע הוורוד, דהיינו  2t/5 וצלעותיו מתייחסות זו לזו ביחס הפיתגוראי כנ"ל, נקבל שאורכי הצלעות הם  בהתאמה

(2t/5)(3/12) = t/10,  (2t/5))(4/12) = 2t/15 , (2t/5)(5/12) = t/6. 

לכן P ,שטח המשולש המבוקש –  ירוק  הקודקודים -הוא   (t/10).(2t/15)/2 = a²/120=P

 פתרון  שאלה  8   – צילום הפתרון של חברנו דוד מ.

 

 פתרון  חידה  8/2020   –

צילום הפתרון של חברנו דוד מ.

 

פתרון חידה 9/2020

מהנתונים יוצא ש    N =3K +2= 3(K+1) -1   לכן N+1 מתחלק ב 3 (בלי שארית). באותו אופן יוצא ש  N+1 מתחלק גם ב 5 וגם ב 7.  למעשה המספר המבוקש  נותן שארית של 1-  מודולו כ"א מהמחלקים הללו.  מכיון שהמספרים 3, 5, 7 זרים זה לזה יוצא שN+1  מתחלק (ללא שארית) במכפלתם 105 =3.5.7. כלומר

=  P.105 N+1 . ועבור P =1 מקבלים את הפתרון המינימלי  104=105-1 = N.

פתרון חידה 10/2020

הנקודה הראשונה  שנבחרת היא  X , 1 >X > 0 . מותר להניח ש  X ≠ 0.5,  X ≠ 0.  ,  X ≠1   (אירועים שהסתברותם אפס).  נטפל בנפרד בכל אחד משני המקרים   X <  0.5   ו   X > 0.5 .כל אחד מהם  מתרחש בהסתברות  0.5 .ברור מנתוני השאלה שאורך כל צלע שמתקבלת לאחר החיתןך/קיפול חייב להיות קטן מ 0.5 !

מקרה א :  X <  0.5  .  במקרה  זה, משיקולי אי שוויון המשולש (דהיינו סכום כל שתי צלעות גדול מהצלע השלישית) על מנת שתתאפשר בניית משולש הנקודה הנבחרת השנייה Y חייבת להיות מימין ל X, אבל  קטנה מ X+0.5,  כלומר    X <  Y  < X +0.5.  ההסתברות לכך היא כאורך הקטע  ולכן  0.5. בנוסף גם נדרש  כמובן

   Y  >  0.5  וגם זה קורה בהסתברות  0.5.  מכיוון שהאירועים שצוי נו ם בלתי תלויים הדדית זה בזה הרי  שההסתברות שהבחירות האלה של X ו Y יאפשרו משולש היא  מכפלת ההסתברויות   0.50.5 x 0.5 x   .  לכן הסיכוי ליצירת משולש הוא במקרה זה 0.125 = 1/8

  מקרה ב :   X  >  0.5 .  השיקולים אנלוגיים לכן  גם כאן קיים סיכוי  של 1/8 להצלחה בבניית משולש.

ביחד מקבלים שהסיכוי הוא      1/4 =  1/8+1/8  , הפתרון לשאלה.

הערה 1 : התקבלו גם פתרונות יפים שמתבססים על שיקולים גיאומטריים.  

הערה 2. : למי שמעוניינים בפתרון לבעייה הכללית של חישוב הסיכוי לבחירת N נקודות על קטע כנ"ל כך שניתן יהיה לבנות מהם מצולע בעל N צלעות להלן קישור לדיון ופתרון. השאלה שלנו נוגעת  כמובן למקרה N=3.

https://www.geeksforgeeks.org/probability-that-the-pieces-of-a-broken-stick-form-a-n-sided-polygon

******************************************************************************************

פתרון חידה 11/2020

אורך צלע הריבוע הכחול הוא שליש מאורך הצלע a של הריבוע השלם .לכן שטח הריבוע  הוא  a²/9.

פתרון חידה 12/2020

להראות שהביטוי   7²⁰²¹⁺13²⁰²¹⁺19²⁰²¹ מתחלק ב 39.

שיטה א . אינדוקציה על כל החזקות האיזוגיות 7²ⁿ⁺¹+ 13²ⁿ⁺¹+19²ⁿ⁺¹, n  שלם חיובי.

עבור  n = 0 ערך הביטוי הוא 39.. מניחים נכונות ל n = k₀  ומראים מכאן נכונות ל   n = k₀ +1 .  ולכן לאו דווקא ל 2021 אלא תמיד, לכל החזקות האיזוגיות!!

שיטה ב.  די בכך שנראה שהביטוי מתחלק בנפרד ב 3 וב 13 ללא שארית שכן 3 ו 13 זרים  זה לזה ומכפלתם היא המספר המבוקש 39!

1.מראים שכל אחת מהחזקות  של 7 נותנת שארית 1 בחילוק  ב 3 . כך גם לגבי חזקות 13 ו 19 .  ביחד סכום שלוש החזקות יהי 1+1+1 בחילוק ב 3 – כלומר ייתחלק ב 3 בעצמו.

2. לגבי התחלקות הביטוי גם ב 13- יש כמובן להראות זאת רק לגבי הסכום 7²⁰²¹⁺19²⁰²¹. נשים לב לכך ש

²⁰²¹ (13-6)+ ²⁰²¹      (13-6 )=I)  = 7²⁰²¹⁺19²⁰²¹

נשתמש בנוסחת הכפל המקוצר הידועה,

a²ⁿ⁺¹ + b²ⁿ⁺¹  = ( a + b)(a²ⁿ– a^2n-1b + a^2n-2b²  – ….. – ab^2n-1 +b²ⁿ)

ולכן בהצבה הברורה  a = (13 -6) , b = (13 +6)

יוצא ש ((I מתחלק בגורם   ((13-6)+(13+6))  = 26  ולכן ב 13. בהוספת 13²⁰²¹ הוכחה הטענה.

פתרון חידות 13/2020 – 15/2020

לפתרון – לחץ/י כאן

פתרון חידות 16/2020 – 18/2020

לפתרון – לחץ/י כאן